一、引 言

LSM-Tree（Log-Structured Merge Tree）是一种高效的键值存储数据结构，广泛应用于NoSQL数据库和大数据处理系统中。其核心思想是通过分层、有序地利用磁盘顺序写入的性能优势，优化写入操作，同时牺牲部分读取性能以换取更高的写入吞吐量。

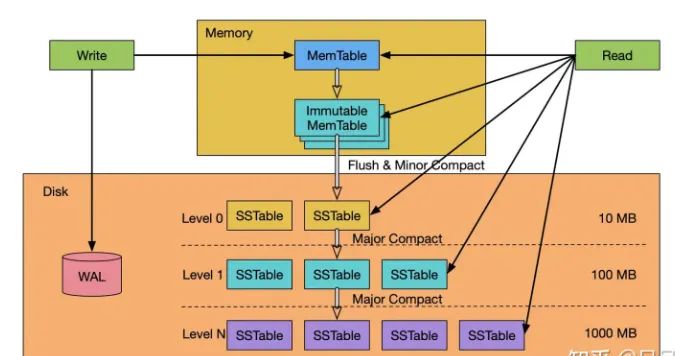
在互联网的各个基础设施中，不论是数据库还是缓存亦或是大数据框架，LSM-Tree这个数据结构都是很常见的身影。

我每天都在使用这个存储引擎，但是对它的了解还流于表面，所以我想要自己实现一次LSM-Tree加深理解。

本次实现我们采用了Zig语言，简要的实现LSM-Tree的核心功能（读写、数据压缩、持久化，不包含MVCC的内容）。

Zig是一种新兴的系统编程语言，其设计目标是提供现代特性的同时保持低复杂性。

本项目极大的受到了Mini-Lsm这个项目的启发，强烈推荐大家学习这个项目！

二、LSM-Treee 核心功能概述

在开始自己编写之前，我先简单介绍一下LSM-Tree（Log-Structured Merge Tree）的架构以及读写流程。

LSM-Tree它结合了日志和索引的特点，优化了写入和读取性能。每次写入都是采用append-only的方式，所以写入性能很高。

而作为代价，追加写入会造成存储放大，LSM-Tree时采用了多层SSTable的方式将数据堆叠在硬盘上。所以需要一个合并压缩的过程来回收过多的空间。

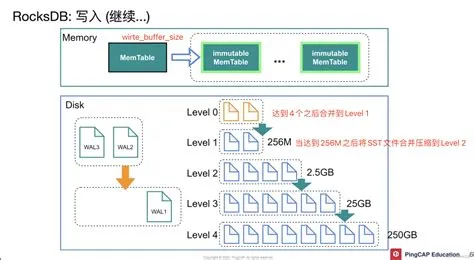
写流程

• 预写日志（WAL） ：写操作首先写入预写日志（WAL），用于记录未提交的数据，确保数据的持久性和一致性。
• MemTable：随后将数据写入内存中的MemTable，MemTable是一个平衡树（如skiplist），支持快速插入和删除操作。
• 触发Compaction：当MemTable达到一定阈值时，会触发后台线程将MemTable中的数据刷入磁盘，生成SSTable文件。
• SSTable：生成的SSTable文件是不可变的，存储在磁盘上，用于后续读取操作。
• 合并操作（Merge） ：当多个SSTable文件达到一定数量时，会触发合并操作，将它们合并为一个更大的SSTable文件，以减少文件数量。

读流程

• MemTable优先：读取操作首先从MemTable中查找数据，因为MemTable是按升序排列的，查找效率较高。
• Block Cache：如果MemTable中未找到数据，则从Block Cache中查找。Block Cache存储了预先加载到内存中的SSTable块，以提高读取性能。
• SSTable查找：如果Block Cache中也未找到数据，则从磁盘上的SSTable文件中查找。Lsm-tree会从最低层（L0）开始查找，逐层向上查找，直到找到目标数据。
• 多版本并发控制（MVCC） ：Lsm-tree支持多版本并发控制，允许同时访问不同版本的数据，从而提高并发性能。

三、核心功能实现

MemTable 实现

首先，我们先实现 LSM 存储引擎的内存结构—Memtable。我们选择跳表实现作为 Memtable 的数据结构，因为它支持无锁的并发读写。我们不会深入介绍跳表的工作原理(Redis的同学应该不陌生这个东西)，简单来说，它是一个易于实现的有序键值映射。

Skiplist的实现非常简单，这里我利用Zig编译时的能力实现了一个泛型版本的跳表src/skiplist.zig，有兴趣的小伙伴可以直接去仓库中参观代码。

基于SkipList的能力，我们即可包装出Memtable的基本功能。

我们这个LSM支持WAL功能的，即写入内存表之前要先写入磁盘日志，方便在意外宕机重启后可以恢复数据。

WAL的能力我就不想自己再实现了，于是从网上扒了一个C的实现（Zig集成C语言非常便捷，可以参考与 C 交互）。

map: Map,
lock: RwLock,
wal: ?Wal,
id: usize,
allocator: std.mem.Allocator,
arena: std.heap.ArenaAllocator,
approximate_size: atomic.Value(usize) = atomic.Value(usize).init(0),

fn putToList(self: *Self, key: []const u8, value: []const u8) !void {
    {
        self.lock.lock();
        defer self.lock.unlock();
        try self.map.insert(kk, vv);
    }

    _ = self.approximate_size.fetchAdd(@intCast(key.len + value.len), .monotonic);
}

fn putToWal(self: *Self, key: []const u8, value: []const u8) !void {
    // [key-size: 4bytes][key][value-size: 4bytes][value]

    if (self.wal) |w| {
        var buf = std.ArrayList(u8).init(self.arena.allocator());

        var bw = buf.writer();
        try bw.writeInt(u32, @intCast(key.len), .big);
        _ = try bw.write(key);
        try bw.writeInt(u32, @intCast(value.len), .big);
        _ = try bw.write(value);
        try w.append(buf.items);
    }
}

// 写入Memtable，先写WAL，再写skiplist table
pub fn put(self: *Self, key: []const u8, value: []const u8) !void {
    try self.putToWal(key, value);
    try self.putToList(key, value);
}

pub fn get(self: *Self, key: []const u8, val: *[]const u8) !bool {
    self.lock.lockShared();
    defer self.lock.unlockShared();
    var vv: []const u8 = undefined;
    if (try self.map.get(key, &vv)) {
        val.* = vv;
        return true;
    }
    return false;
}

注意到这里我们没有实现删除的功能，这里我仿照了RocksDB中的墓碑机制，用空值代表删除，所以删除被put(key, “”)取代。

SSTable

接下来，我们就着手开始实现LSM中另外一个重要元素 — SSTable。

SSTable（Sorted String Table）是一种不可变的（Immutable）磁盘文件，内部按Key有序排列，存储键值对数据。每个SSTable文件生成后不再修改，更新和删除操作通过追加新记录或标记删除，最终通过合并（Compaction）清理冗余数据。
每当LSM-Tree中的MemTable体积超出阈值，就会将内存中的数据写入SsTable。

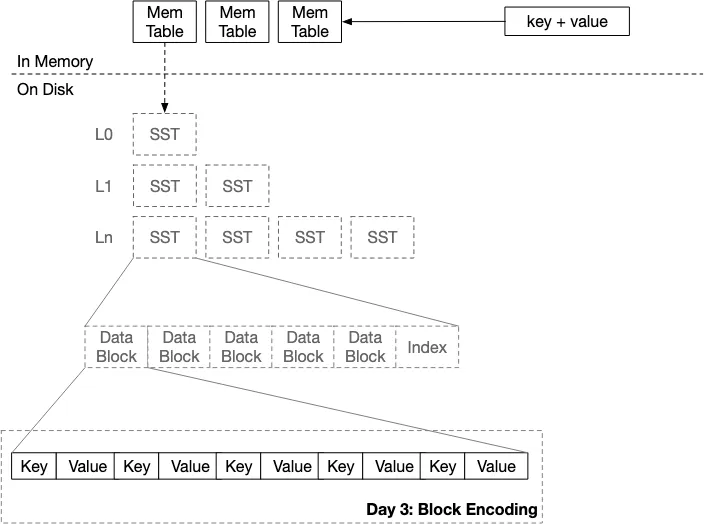
每个SSTable由多个Block组成，每个Block是一组KV的package。

Block的编码格式如下：

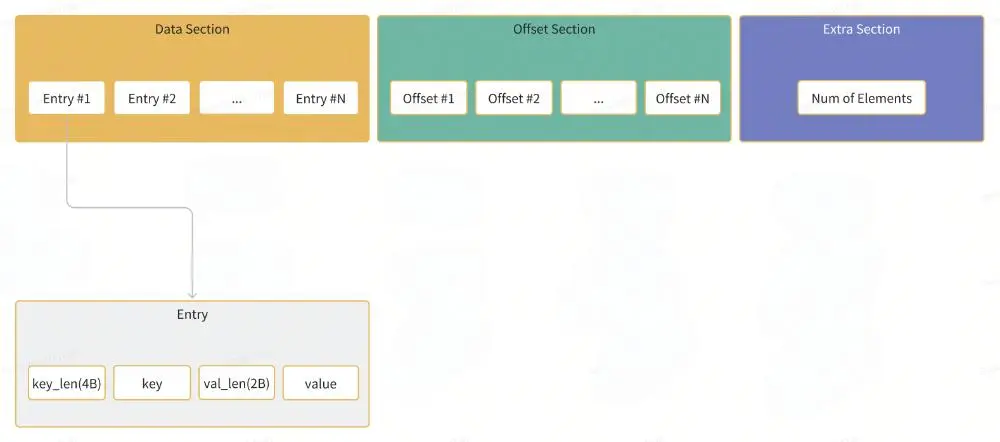
为了构建一个Block，我们实现了一个BlockBuilder的模块，这部分代码见src/block.zig：

pub const Block = struct {
    data_v: std.ArrayList(u8),
    offset_v: std.ArrayList(u16),
}

pub const BlockBuilder = struct {
    allocator: std.mem.Allocator,
    offset_v: std.ArrayList(u16),
    data_v: std.ArrayList(u8),
    block_size: usize,
    first_key: []u8,
    
    pub fn add(self: *Self, key: []const u8, value: ?[]const u8) !bool {
        std.debug.assert(key.len > 0); // key must not be empty

        const vSize = if (value) |v| v.len else 0;
        
        if ((self.estimated_size() + key.len + vSize + 3 * @sizeOf(u16) > self.block_size) and !self.is_empty()) {
            return false;
        }
        try self.doAdd(key, value);

        if (self.first_key.len == 0) {
            self.first_key = try self.allocator.dupe(u8, key);
        }
        return true;
    }

    fn doAdd(self: *Self, key: []const u8, value: ?[]const u8) !void {
        // add the offset of the data into the offset array
        try self.offset_v.append(@intCast(self.data_v.items.len));
        const overlap = calculate_overlap(self.first_key, key);

        var dw = self.data_v.writer();
        // encode key overlap
        try dw.writeInt(u16, @intCast(overlap), .big);
        // encode key length
        try dw.writeInt(u16, @intCast(key.len - overlap), .big);

        // encode key content
        _ = try dw.write(key[overlap..]);
        // encode value length
        if (value) |v| {
            try dw.writeInt(u16, @intCast(v.len), .big);
            // encode value content
            _ = try dw.write(v);
        } else {
            try dw.writeInt(u16, 0, .big);
        }
    }

    pub fn build(self: *Self) !Block {
        if (self.isEmpty()) {
            @panic("block is empty");
        }
        return Block.init(
            try self.data_v.clone(),
            try self.offset_v.clone(),
        );
    }
}

可能有同学注意到，我们写key的时候没有直接将key值写入，而且只写了key与当前block的第一个key不重叠的suffix部分。由于block中的key都是有序的，所以一个block中的key有很大概率是前缀类似的，所以这里是一个空间优化的小技巧，例如：

Key: foo, foo1, foo2, foo3 …

我们写入block时，只需要写：

foo|1|2|3|…
很多有序表的实现中都会用到这个小技巧。

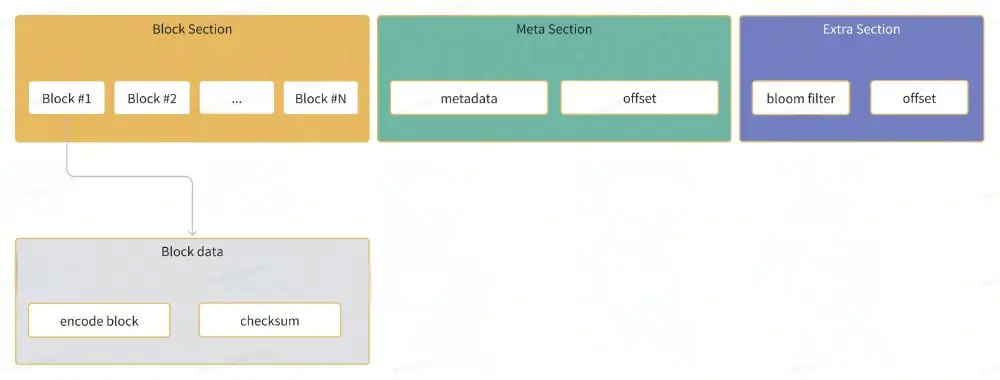
有了block的实现，我们可以进一步来定义SSTable的格式。一个SSTable由多个Block、block元数据以及布隆过滤器构成。

布隆过滤器是一种概率性数据结构，用于维护一组键。您可以向布隆过滤器中添加键，并且可以知道在添加到布隆过滤器中的键集中可能存在或必须不存在的键。

在SSTable中添加布隆过滤器可以有效提升查询key的效率。

元数据包含了block的第一个与最后一个key以及block在sst中的offset信息，记录元数据主要为了在后续的检索中可以快速定位某个key落在哪个block中。

同样的套路，为了构建SSTable，我们先实现一个SSTableBuilder，部分代码见src/ss_table.zig

pub const SsTableBuilder = struct {
    allocator: std.mem.Allocator,
    builder: BlockBuilder, // 刚才实现的block构建装置
    first_key: ?[]const u8,
    last_key: ?[]const u8,
    meta: std.ArrayList(BlockMeta),
    block_size: usize,
    data: std.ArrayList(u8),
    bloom: BloomFilterPtr, // 布隆过滤器
    
    pub fn add(self: *Self, key: []const u8, value: []const u8) !void {
        try self.setFirstKey(key);
        try self.bloom.get().insert(key); // 写入布隆过滤器

        if (try self.builder.add(key, value)) {
            try self.setLastKey(key);
            return;
        }
        // block is full
        try self.finishBlock();
        std.debug.assert(try self.builder.add(key, value));
        try self.resetFirstKey(key);
        try self.setLastKey(key);
    }
    
    // 写入一个block的数据
    fn finishBlock(self: *Self) !void {
        if (self.builder.isEmpty()) {
            return;
        }
        var bo = self.builder;
        // reset block
        defer bo.reset();

        self.builder = BlockBuilder.init(self.allocator, self.block_size);
        var blk = try bo.build();
        defer blk.deinit();
        const encoded_block = try blk.encode(self.allocator); // block序列化
        defer self.allocator.free(encoded_block);
        
        // 记录block的元数据
        try self.meta.append(.{
            .allocator = self.allocator,
            .offset = self.data.items.len,
            .first_key = try self.allocator.dupe(u8, self.first_key.?),
            .last_key = try self.allocator.dupe(u8, self.last_key.?),
        });
        const cksm = hash.Crc32.hash(encoded_block); // 写入4b的校验值
        try self.data.appendSlice(encoded_block);
        try self.data.writer().writeInt(u32, cksm, .big);
    }
    
    // 构建为一个SSTable
    pub fn build(
        self: *Self,
        id: usize,
        block_cache: ?BlockCachePtr, // 读取block数据的缓存，减少block的反序列化成本
        path: []const u8,
    ) !SsTable {
        var arena = std.heap.ArenaAllocator.init(self.allocator);
        defer arena.deinit();
        const allocator = arena.allocator();

        try self.finishBlock();
        const w = self.data.writer();
        
        // 写入元数据及其offset
        const meta_offset = self.data.items.len;
        const meta_b = try BlockMeta.batchEncode(self.meta.items, allocator);
        _ = try w.write(meta_b);
        try w.writeInt(u32, @intCast(meta_offset), .big);

        // 写入布隆过滤器及其offset
        const bloom_offset = self.data.items.len;
        const encoded_bloom = try self.bloom.get().encode(allocator);
        _ = try w.write(encoded_bloom);
        try w.writeInt(u32, @intCast(bloom_offset), .big);
        
        
        const file = try FileObject.init(path, self.data.items);
        errdefer file.deinit();

        const fk = self.meta.items[0].first_key;
        const lk = self.meta.getLast().last_key;

        return .{
            .allocator = self.allocator,
            .file = file,
            .block_metas = try self.meta.toOwnedSlice(),
            .meta_offset = meta_offset,
            .block_cache = block_cache,
            .bloom = self.bloom.clone(),
            .id = id,
            .first_key = try self.allocator.dupe(u8, fk),
            .last_key = try self.allocator.dupe(u8, lk),
            .max_ts = 0,
        };
    }
}

Write

有了SSTable和MemTable，我们就有了LSM-Tree需要的两个最重要的材料，后续的读写不过是对这两类材料的组合拼装。

在实现写操作之前，我们先假想一下LSM-Tree的数据结构:

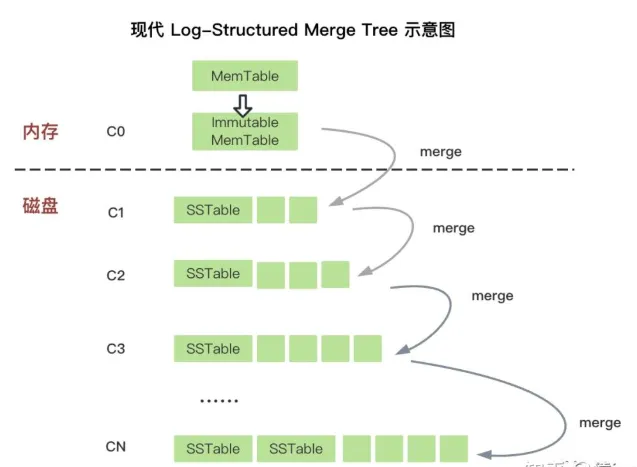
• 首先我们需要一个数据结构存储当前MemTable、冷MemTables和多层的SST，如下图所示。
  图片
• 其次我们需要一个锁用于同步上述数据结构的读写行为。
• 我们还需要一个SSTable的自增id。
• 最后还需要一些必要的配置，例如存储路径、线程管理器等。

最终，我们实现的LSM数据结构如下：

pub const StorageState = struct {
    allocator: std.mem.Allocator,
    mem_table: MemTablePtr, // 当前正在写的MemTable
    imm_mem_tables: std.ArrayList(MemTablePtr), // 冷MemTable数组
    l0_sstables: std.ArrayList(usize), // 第一层的SSTable数组
    levels: std.ArrayList(std.ArrayList(usize)), // 后续多层的SSTable数组
    sstables: std.AutoHashMap(usize, SsTablePtr), // sst_id => SSTable
}

pub const StorageInner = struct {
    const Self = @This();

    allocator: std.mem.Allocator,
    state: StorageState,
    state_lock: std.Thread.RwLock = .{},
    next_sst_id: atomic.Value(usize),
    path: []const u8,
    options: StorageOptions,
    compaction_controller: CompactionController,
    block_cache: BlockCachePtr,
    terminate: std.Thread.ResetEvent = .{},
    wg: std.Thread.WaitGroup = .{},
}

先不考虑逐层压缩的逻辑，只考虑一层SSTable的简单情况，写逻辑可以简化为如下流程：

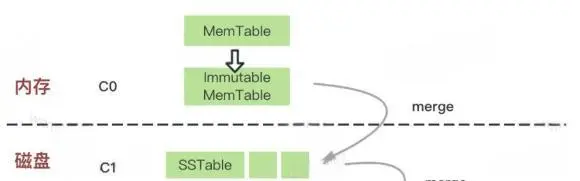
• 写入State中的MemTable

pub fn writeBatch(self: *Self, records: []const WriteBatchRecord) !void {
   for (records) |record| {
       switch (record) {
           .put => |pp| {
               try self.state.getMemTable().put(pp.key, pp.value);
           },
           .delete => |dd| {
               // we use "" as the tombstone value
               try self.state.getMemTable().put(dd, "");
           },
       }
       // 尝试把当前MemTable压入冷数据
       try self.tryFreeze(self.state.getMemTable().getApproximateSize());
   }
}

• 当MemTable体积超出阈值，压入冷MemTable数组，重置当前MemTable

fn forceFreezeMemtable(self: *Self) !void {
    const next_sst_id = self.getNextSstId();
    
    // 生成一个新的MemTable
    var new_mm: MemTable = undefined;
    {
        if (self.options.enable_wal) {
            const mm_path = try pathOfWal(self.allocator, self.path, next_sst_id);
            defer self.allocator.free(mm_path);
            new_mm = MemTable.init(next_sst_id, self.allocator, mm_path);
        } else {
            new_mm = MemTable.init(next_sst_id, self.allocator, null);
        }
    }
    errdefer new_mm.deinit();

    var old_mm: *MemTable = undefined;
    {
        self.state_lock.lock();
        defer self.state_lock.unlock();
        var old_mm_ptr = self.state.mem_table;
        old_mm = old_mm_ptr.get();
        defer old_mm_ptr.release();
        self.state.mem_table = try MemTablePtr.create(self.allocator, new_mm);
        
        // 将写满的MemTable压入冷数据
        try self.state.imm_mem_tables.append(old_mm_ptr.clone()); // newer memtable is inserted at the end
    }
    // TIPS：把磁盘同步放在锁的范围外面，降低锁的覆盖
    try old_mm.syncWal();
}

• 当冷MemTable数组大小超出配置阈值，触发SSTable落盘，弹出最冷的MemTable，写入磁盘SSTable，并记录在L0的SSTable数组中。这一过程是在一个线程中定时触发

pub fn flushNextMemtable(self: *Self) !void {
    std.debug.assert(self.state.imm_mem_tables.items.len > 0);
    var to_flush_table: *MemTable = undefined;
    {
        self.state_lock.lockShared();
        defer self.state_lock.unlockShared();
        // oldest memtable is at the index 0
        to_flush_table = self.state.imm_mem_tables.items[0].load();
    }

    // 将最冷的MemTable构建为SSTable
    var builder = try SsTableBuilder.init(self.allocator, self.options.block_size);
    defer builder.deinit();

    const sst_id = to_flush_table.id;
    try to_flush_table.flush(&builder);

    const sst_path = try self.pathOfSst(sst_id);
    defer self.allocator.free(sst_path);
    var sst = try builder.build(sst_id, self.block_cache.clone(), sst_path);
    errdefer sst.deinit();

    // add the flushed table to l0_sstables
    {
        self.state_lock.lock();
        defer self.state_lock.unlock();

        var m = self.state.imm_mem_tables.orderedRemove(0);
        defer m.deinit();
        std.debug.assert(m.load().id == sst_id);

        // newest sstable is at the end
        try self.state.l0_sstables.append(sst_id);
        try self.state.sstables.put(sst.id, try SsTablePtr.create(self.allocator, sst));
    }
}

当然，这里只实现了一半的写逻辑，数据停留在L0的SST中，后续的多层SST还没有使用。

剩下一半的写逻辑会在数据压缩的章节中介绍。

Iterators

写入的过程比较好理解，但是读就略微复杂了，以上面我们实现的写结果为例子，最终我们的数据沉淀在一个3层的数据结构中，要如何高效的从其中检索数据呢？

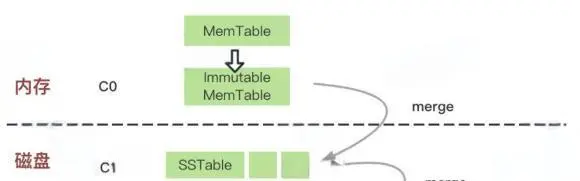
如同写过程一般，读过程也是对各个基础单元(MemTable、SSTable、Block)读过程的组合，为了方便组合逻辑，我们要先统一各个模块的读行为。

在LSM-Tree中，所有的读行为都定义为了如下的Interface（Zig中没trait或者Interface，所以这里实例代码我用Rust描述）：

pub trait StorageIterator {
    /// Get the current value.
    fn value(&self) -> &[u8];

    /// Get the current key.
    fn key(&self) -> &[u8];

    /// Check if the current iterator is empty.
    fn is_empty(&self) -> bool;

    /// Move to the next position.
    fn next(&mut self) -> anyhow::Result<()>;

    /// Number of underlying active iterators for this iterator.
    fn num_active_iterators(&self) -> usize {
        1
    }
}

我们首先对MemTable、SSTable、Block这些模块实现读接口，代码可见：src/MemTable.zig，src/block.zig，src/ss_table.zig，这里单独简单介绍下SSTable的读接口实现思路，其他的模块实现思路类似，感兴趣的直接阅读源码即可。

pub const SsTableIterator = struct {
    allocator: std.mem.Allocator,
    table: SsTablePtr,
    blk: BlockPtr,
    blk_iterator: BlockIteratorPtr,
    blk_idx: usize,

    const Self = @This();


    pub fn initAndSeekToFirst(allocator: std.mem.Allocator, table: SsTablePtr) !Self {
        const s = try seekToFirstInner(allocator, table);
        return .{
            .allocator = allocator,
            .table = table,
            .blk_iterator = s.blk_iter,
            .blk = s.blk,
            .blk_idx = 0,
        };
    }

    pub fn initAndSeekToKey(allocator: std.mem.Allocator, table: SsTablePtr, k: []const u8) !Self {
        const b = try seekToKeyInner(allocator, table, k);
        return .{
            .allocator = allocator,
            .table = table,
            .blk_iterator = b.blk_iter,
            .blk_idx = b.blk_idx,
            .blk = b.blk,
        };
    }

    fn seekToFirstInner(allocator: std.mem.Allocator, table: SsTablePtr) !struct {
        blk: BlockPtr,
        blk_iter: BlockIteratorPtr,
    } {
        var blk = try table.get().readBlockCached(0, allocator); // 读取第一个block
        errdefer blk.release();
        var blk_iter = try BlockIterator.createAndSeekToFirst(allocator, blk.clone());
        errdefer blk_iter.deinit();

        return .{
            .blk = blk,
            .blk_iter = try BlockIteratorPtr.create(allocator, blk_iter), // 从SSTable的读接口转换为Block的读接口
        };
    }

    fn seekToKeyInner(allocator: std.mem.Allocator, table: SsTablePtr, k: []const u8) !struct {
        blk_idx: usize,
        blk: BlockPtr,
        blk_iter: BlockIteratorPtr,
    } {
        const table_ptr = table.get();
        var blk_idx = try table_ptr.findBlockIndex(k);
        var blk = try table_ptr.readBlockCached(blk_idx, allocator);
        errdefer blk.deinit();
        var blk_iter = try BlockIterator.createAndSeekToKey(allocator, blk.clone(), k);
        errdefer blk_iter.deinit();
        var blk_iter_ptr = try BlockIteratorPtr.create(allocator, blk_iter);
        errdefer blk_iter_ptr.release();

        // 如果当前block读完了，跳到下一个block，并生成block的读接口
        if (blk_iter.isEmpty()) {
            blk_idx += 1;
            if (blk_idx < table_ptr.numBlocks()) {
                {
                    blk.deinit();
                    blk_iter.deinit();
                }
                var blk2 = try table_ptr.readBlockCached(blk_idx, allocator);
                errdefer blk2.deinit();
                var blk_iter2 = try BlockIterator.createAndSeekToFirst(allocator, blk2.clone());
                errdefer blk_iter2.deinit();

                return .{
                    .blk_idx = blk_idx,
                    .blk_iter = try BlockIteratorPtr.create(allocator, blk_iter2),
                    .blk = blk2,
                };
            }
        }
        return .{
            .blk_idx = blk_idx,
            .blk_iter = blk_iter_ptr,
            .blk = blk,
        };
    }

    pub fn key(self: Self) []const u8 {
        return self.blk_iterator.get().key();
    }

    pub fn value(self: Self) []const u8 {
        return self.blk_iterator.get().value();
    }

    pub fn isEmpty(self: Self) bool {
        return self.blk_iterator.get().isEmpty();
    }

    pub fn next(self: *Self) !void {
        try self.blk_iterator.get().next();
        // 若当前的Block读完了，就跳到下一个block，并生成Block读接口。
        if (self.blk_iterator.get().isEmpty()) {
            self.blk_idx += 1;
            if (self.blk_idx < self.table.get().numBlocks()) {
                self.reset();
                const blk = try self.table.get().readBlockCached(self.blk_idx, self.allocator);
                const blk_iter = try BlockIterator.createAndSeekToFirst(self.allocator, blk.clone());
                self.blk = blk;
                self.blk_iterator = try BlockIteratorPtr.create(self.allocator, blk_iter);
            }
        }
    }
};

有了几个基本元素的读接口之后，我们便遇到第一个问题：我们如何对多个MemTable做读检索？

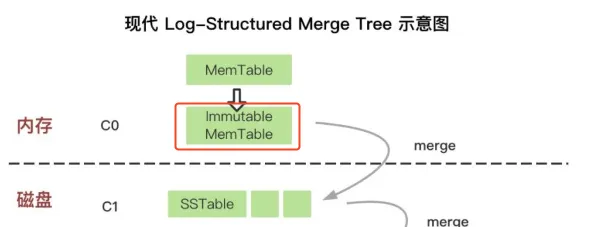
这个时候，我们需要一个新的数据结构来实现多个读实例的合并检索---- MergeIterator

MergeIterator在内部维护一个二叉堆。堆中数据的优先级如下：

当各个迭代器key不同时，具有最小key的迭代器最优。当多个迭代器有相同的当前key时，最新的迭代器一个最优。

假设我们有如下MemTable（iter1最新，iter3最旧）:

iter1: b->del, c->4, d->5
iter2: a->1, b->2, c->3
iter3: e->4

经过合并后迭代器结果应该为：

a最小，iter2优先迭代
iter2迭代一次后，iter1与iter2 key相同，iter1优先迭代，b->2跳过
c最小，iter1优先迭代，iter2中c->3跳过
d最小，iter1优先迭代
只剩iter3，迭代iter3

最终结果：a->1, b->del, c->4, d->5, e->4

实现代码如下：

// 标准库中有二叉堆实现
const IteratorHeap = std.PriorityQueue(*HeapWrapper, Comparer.Context, Comparer.cmp);

allocator: std.mem.Allocator,
q: IteratorHeap,
current: ?*HeapWrapper,

pub fn init(allocator: std.mem.Allocator, iters: std.ArrayList(StorageIteratorPtr)) !Self {
    var q = IteratorHeap.init(allocator, .{});
    if (iters.items.len == 0) {
        return Self{
            .allocator = allocator,
            .q = q,
            .current = null,
        };
    }

    // PS: the last iter has the highest priority
    // 按顺序写入二叉堆
    for (iters.items, 0..) |sp, i| {
        if (!sp.load().isEmpty()) {
            const hw = try allocator.create(HeapWrapper);
            errdefer allocator.destroy(hw);
            hw.* = HeapWrapper.init(i, sp.clone());
            try q.add(hw);
        }
    }

    const cc = q.removeOrNull();
    return Self{
        .allocator = allocator,
        .q = q,
        .current = cc,
    };
}

pub fn key(self: Self) []const u8 {
    return self.current.?.key();
}

pub fn value(self: Self) []const u8 {
    return self.current.?.value();
}

pub fn isEmpty(self: Self) bool {
    if (self.current) |cc| {
        return cc.isEmpty();
    }
    return true;
}

pub fn next(self: *Self) !void {
    const cc = self.current.?;
    while (true) {
        if (self.q.peek()) |ii| {
            std.debug.assert(!ii.isEmpty());
            // 如果优先堆头部迭代器A和当前正在生效的迭代器B的key相同，让迭代器A跳过重复key
            if (std.mem.eql(u8, cc.key(), ii.key())) {
                try ii.next();
                if (ii.isEmpty()) {
                    _ = self.q.remove();
                    ii.deinit();
                    self.allocator.destroy(ii);
                }
            } else {
                break;
            }
        }
        break;
    }

    try cc.next(); // 迭代当前迭代器

    // 如果当前优先迭代器迭代完了，就从堆中弹出最优迭代器
    if (cc.isEmpty()) {
        defer {
            cc.deinit();
            self.allocator.destroy(cc);
        }
        if (self.q.removeOrNull()) |h| {
            self.current = h;
        } else {
            self.current = null;
        }
        return;
    }

    // 将当前迭代器写回二叉堆，重新计算最优迭代器
    try self.q.add(cc); 
    self.current = self.q.removeOrNull();
}

有了MergeIterator这个工具，我们具备了在多个MemTable和多个SSTable中迭代检索的能力，但是还有个问题，我们当前有两个MergeIterator，应该如何在两个迭代器中执行迭代任务？

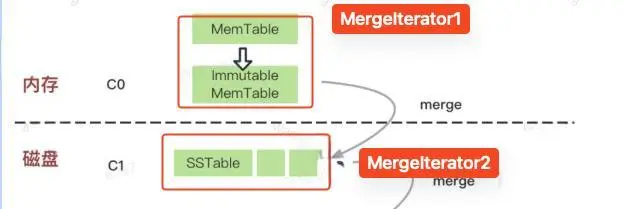
此时，我们再引入一个新的数据结构：TwoMergeIterator，这个是MergeIterator在元素只有两个的情况下的简化版。

TwoMergeIterator由两个迭代器构成，一个高优一个低优，每次迭代优先迭代高优，当key相同时，优先迭代高优。实现如下：

pub const TwoMergeIterator = struct {
    a: StorageIteratorPtr,
    b: StorageIteratorPtr,
    choose_a: bool,

    // 选择两个迭代器中key更小的迭代器
    fn chooseA(a: *StorageIterator, b: *StorageIterator) bool {
        if (a.isEmpty()) {
            return false;
        }
        if (b.isEmpty()) {
            return true;
        }
        return std.mem.lessThan(u8, a.key(), b.key());
    }

    // key相同时，跳过低优中的key
    fn skipB(self: *TwoMergeIterator) !void {
        const ap = self.a.load();
        const bp = self.b.load();
        if (!ap.isEmpty() and !bp.isEmpty() and std.mem.eql(u8, ap.key(), bp.key())) try bp.next();
    }

    pub fn init(a: StorageIteratorPtr, b: StorageIteratorPtr) !TwoMergeIterator {
        var iter = TwoMergeIterator{
            .a = a,
            .b = b,
            .choose_a = false,
        };
        try iter.skipB();
        iter.choose_a = chooseA(iter.a.load(), iter.b.load());
        return iter;
    }

    pub fn deinit(self: *TwoMergeIterator) void {
        self.a.release();
        self.b.release();
    }

    pub fn key(self: TwoMergeIterator) []const u8 {
        if (self.choose_a) {
            std.debug.assert(!self.a.load().isEmpty());
            return self.a.load().key();
        }
        std.debug.assert(!self.b.load().isEmpty());
        return self.b.load().key();
    }

    pub fn value(self: TwoMergeIterator) []const u8 {
        if (self.choose_a) {
            std.debug.assert(!self.a.load().isEmpty());
            return self.a.load().value();
        }
        std.debug.assert(!self.b.load().isEmpty());
        return self.b.load().value();
    }

    pub fn isEmpty(self: TwoMergeIterator) bool {
        if (self.choose_a) {
            return self.a.load().isEmpty();
        }
        return self.b.load().isEmpty();
    }

    pub fn next(self: *TwoMergeIterator) !void {
        if (self.choose_a) {
            try self.a.load().next();
        } else {
            try self.b.load().next();
        }
        try self.skipB();
        self.choose_a = chooseA(self.a.load(), self.b.load());
    }
};

至此，我们读行为所需要的武器就完备了！

Read/Scan

让我们再来看看LSM的架构图：

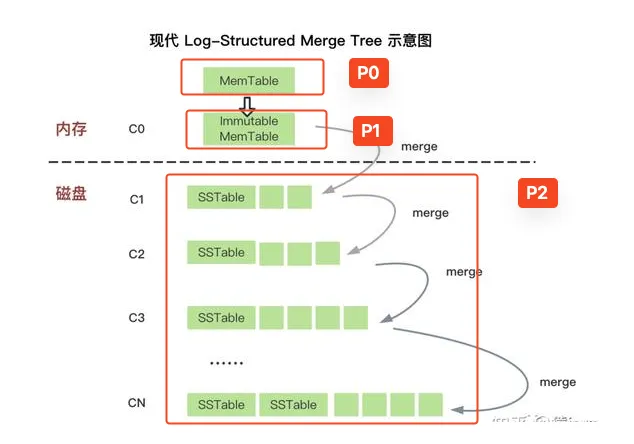
我们将每个数据层中的数据标上优先级，由于LSM-Tree是append-only的，所以优先级越高的数据层中数据越新。

所以我们的读策略也很明显：按照上图中P0至P2依次检索，这部分代码实现见src/storage.zig。

• 读MemTable

// search in memtable
if (try self.state.getMemTable().get(key, value)) {
    if (value.*.len == 0) {
        // tomestone
        return false;
    }
    return true;
}

• 读Immutable MemTable

// search in imm_memtables

self.state_lock.lockShared();
defer self.state_lock.unlockShared();
for (self.state.imm_mem_tables.items) |imm_table| {
    if (try imm_table.load().get(key, value)) {
        if (value.*.len == 0) {
            // tomestone
            return false;
        }
        return true;
    }
}

• 读LV0~LVmax SSTables

// 收集L0中的迭代器
var l0_iters = std.ArrayList(StorageIteratorPtr).init(self.allocator);
defer {
    for (l0_iters.items) |iter| {
        var ii = iter;
        ii.release();
    }
    l0_iters.deinit();
}
{
    self.state_lock.lockShared();
    defer self.state_lock.unlockShared();
    for (self.state.l0_sstables.items) |sst_id| {
        const sst = self.state.sstables.get(sst_id).?;
        if (try sst.load().mayContain(key)) {
            var ss_iter = try SsTableIterator.initAndSeekToKey(self.allocator, sst.clone(), key);
            errdefer ss_iter.deinit();
            try l0_iters.append(try StorageIteratorPtr.create(self.allocator, .{ .ss_table_iter = ss_iter }));
        }
    }
}

// 收集Levels中的迭代器
var level_iters: std.ArrayList(StorageIteratorPtr) = undefined;
{
    self.state_lock.lockShared();
    defer self.state_lock.unlockShared();
    level_iters = try std.ArrayList(StorageIteratorPtr).initCapacity(
        self.allocator,
        self.state.levels.items.len,
    );
    for (self.state.levels.items) |level| {
        var level_ssts = try std.ArrayList(SsTablePtr).initCapacity(self.allocator, level.items.len);
        errdefer level_ssts.deinit();
        for (level.items) |sst_id| {
            const sst = self.state.sstables.get(sst_id).?;
            if (try mayWithinTable(key, sst)) {
                try level_ssts.append(sst.clone());
            }
        }
        if (level_ssts.items.len > 0) {
            var level_iter = try SstConcatIterator.initAndSeekToKey(
                self.allocator,
                level_ssts,
                key,
            );
            errdefer level_iter.deinit();
            try level_iters.append(try StorageIteratorPtr.create(self.allocator, .{ .sst_concat_iter = level_iter }));
        }
    }
}

// 将多个迭代器合并为一个TwoMergeIterator
var l0_merge_iter = try MergeIterators.init(self.allocator, l0_iters);
errdefer l0_merge_iter.deinit();

var levels_merge_iter = try MergeIterators.init(self.allocator, level_iters);
errdefer levels_merge_iter.deinit();

var iter = try TwoMergeIterator.init(
    try StorageIteratorPtr.create(self.allocator, .{ .merge_iterators = l0_merge_iter }),
    try StorageIteratorPtr.create(self.allocator, .{ .merge_iterators = levels_merge_iter }),
);
defer iter.deinit();

if (iter.isEmpty()) {
    return false;
}

if (std.mem.eql(u8, iter.key(), key) and iter.value().len > 0) {
    value.* = iter.value();
    return true;
}

压缩

在上一节的写过程中，我们实现了从内存表到Level0的SSTable堆叠。

随着写入的持续，Lv0的SSTable会越来越多，这个时候就需要我们将Lv0中的数据合并写入至Lv2，并依次类推重复这个过程，直到堆叠到最深的层数，这个逐层合并数据的过程就是数据压缩。

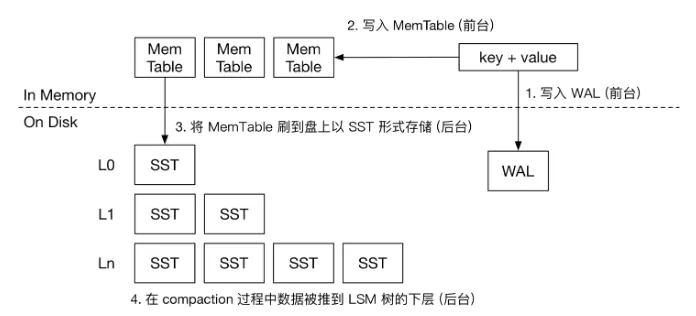
LSM-Tree中数据压缩的过程大致如下：

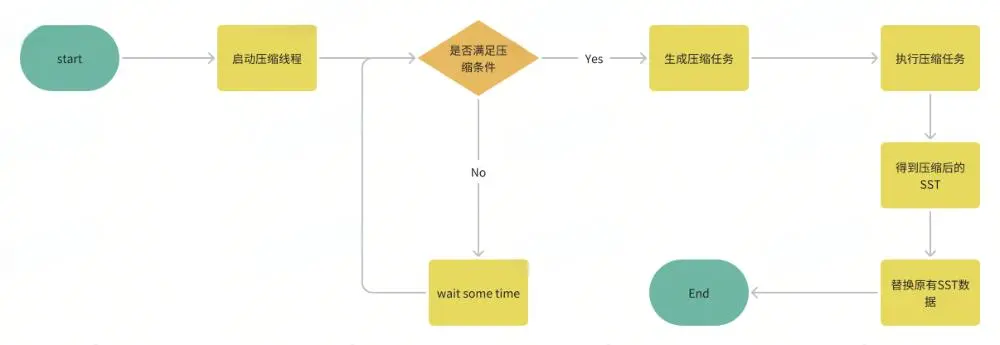
具体的实现代码可见src/compact.zig，src/storage.zig。

简单分层压缩与原始 LSM 论文中的压缩策略相似。它为 LSM 树维护多个层级。当一个层级太大时，它会将此层级的所有 SST 与下一层合并。压缩策略由 3 个参数控制：

• size_ratio_percent：【文件低级数量/文件高级数量】，当实际计算的值低于此阈值时触发压缩。假设这里我们设置为60%，当L0中SST数量为2，L1中SST数量为1，此时ratio为1/2 = 50% < 60%，此时我们应该将L0压缩合并至L1。
• level0_file_num_compaction_trigger: 第一层SSTable达到多少后触发压缩。因为这是最高层，没法与更高层比较，只能固定触发压缩。
• max_levels: 顾名思义，最大的层数限制。

做好这些准备工作，我们可以逐步实现压缩逻辑：

• 生成压缩任务：

pub const SimpleLeveledCompactionController = struct {
    options: SimpleLeveledCompactionOptions,

    pub fn generateCompactionTask(self: SimpleLeveledCompactionController, state: *storage.StorageState) !?SimpleLeveledCompactionTask {
        if (self.options.max_levels == 1) {
            return null;
        }

        var level_sizes = std.ArrayList(usize).init(state.allocator);
        defer level_sizes.deinit();

        try level_sizes.append(state.l0_sstables.items.len);
        for (state.levels.items) |level| {
            try level_sizes.append(level.items.len);
        }

        // 如果Lv0中SST数量超出阈值，触发L0级别压缩
        if (state.l0_sstables.items.len >= self.options.level0_file_num_compaction_trigger) {
            std.debug.print("compaction of L0 to L1 because L0 has {d} SSTS >= {d}\n", .{ state.l0_sstables.items.len, self.options.level0_file_num_compaction_trigger });
            return .{
                .upper_level = null,
                .upper_level_sst_ids = try state.l0_sstables.clone(),
                .lower_level = 1,
                .lower_level_sst_ids = try state.levels.items[0].clone(),
                .is_lower_level_bottom = false,
            };
        }

        // 计算Lv[n+1]/lv[n]，如果比例小于阈值，触发Lv[n]级别压缩
        for (1..self.options.max_levels) |level| {
            const lower_level = level + 1;
            if (level_sizes.items[level] == 0) {
                continue;
            }
            const size_ration = level_sizes.items[lower_level] * 100 / level_sizes.items[level];
            if (size_ration < self.options.size_ration_percent) {
                std.debug.print("compaction of L{d} to L{d} because L{d} size ratio {d} < {d}\n", .{ level, lower_level, level, size_ration, self.options.size_ration_percent });
                return .{
                    .upper_level = level,
                    .upper_level_sst_ids = try state.levels.items[level - 1].clone(),
                    .lower_level = lower_level,
                    .lower_level_sst_ids = try state.levels.items[lower_level - 1].clone(),
                    .is_lower_level_bottom = lower_level == self.options.max_levels,
                };
            }
        }

        return null;
    }
}

• 执行压缩任务：

有了上一小节中读过程的介绍，多层数据的压缩过程就很好理解了。

例如我们想将L1与L2的SSTable合并压缩至L2，我们只需要把L1和L2的数据放在一起创造一个迭代器，再持续从该迭代器中读出数据写入新的SSTable中，这个过程保证了新的SSTable中数据不重复且有序。

fn compactSimple(self: *Self, task: SimpleLeveledCompactionTask) !std.ArrayList(SsTablePtr) {
    if (task.upper_level) |_| {
        var upper_ssts = try std.ArrayList(SsTablePtr).initCapacity(
            self.allocator,
            task.upper_level_sst_ids.items.len,
        );
        var lower_ssts = try std.ArrayList(SsTablePtr).initCapacity(
            self.allocator,
            task.lower_level_sst_ids.items.len,
        );

        self.state_loc